Background
Generative Adversarial Network (GAN)
A GAN consists of two networks: a generator network G and a discriminator network D [1]. The generator G takes as input a random noise z sampled from a prior distribution pz and output a fake sample G(z). The discriminator D takes as input either a sample drawn from real data or generated by the generator and outputs a scalar indicating its authenticity.
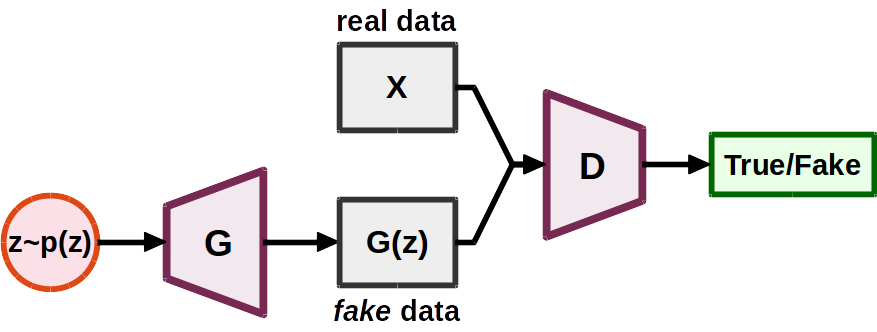
The adversarial setting goes like this:
- D tries to tell the fake samples from the real samples
- G tries to fool D (to make D misclassify the generated, fake samples as real ones)
In general, most GAN loss functions proposed in the literature take the following form:
maxD Ex~pd [ f(D(x)) ] + Ex~pg [ g(D(x)) ]
minG Ex~pg [ h(D(x)) ]
Here, pd denotes the data distribution and pg denotes the model distribution implicitly defined by G(z) when z~pz. Moreover, f, g and h are real functions defined on the data space (i.e., X → ℝ), and we will refer to them as the component functions.
Conditional Generative Adversarial Networks (CGAN)
In a conditional GAN (CGAN) [2], both the generator G and the discriminator D are now conditioned on some variable y. Typical (x, y) pairs include (data, labels), (data, tags), (image, image).
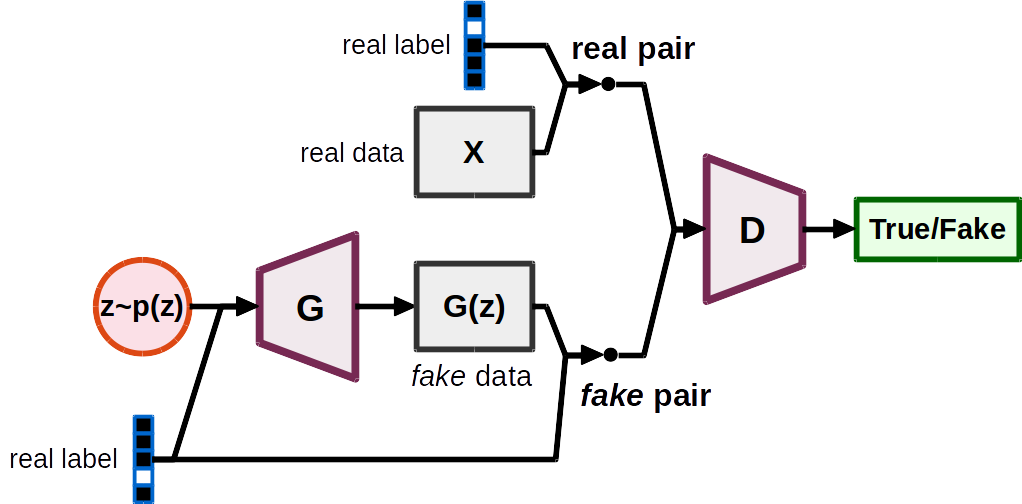
Gradient penalties
As the discriminator is often found to be too strong to provide reliable gradients to the generator, one regularization approach is to use some gradient penalties to constrain the modeling capability of the discriminator.
Most gradient penalties proposed in the literature take the following form:
λ Ex~px [ R( ||∇x D(x)|| ) ]
Here, the penalty weight λ ∈ ℝ is a pre-defined constant, and R(·) is a real function. The distribution px defines where the gradient penalties are enforced. Note that this term will be added to the loss function as a regularization term for the discriminator.
Here are some common gradient penalties and their px and R(·).
| gradient penalty type | px | R(x) |
|---|---|---|
| coupled gradient penalties [3] | pd + U[0, 1] (pg − pd) | (x − k)2 or max(x, k) |
| local gradient penalties [4] | pd + c N[0, I] | (x − k)2 or max(x, k) |
| R1 gradient penalties [5] | pd | x |
| R2 gradient penalties [5] | pg | x |
Spectral normalization
Spectral normalization [6] is another regularization approach for GANs. It normalizes the spectral norm of each layer in a neural network to enforce the Lipschitz constraints. While the gradient penalties impose local regularizations, the spectral normalization imposes a global regularization on the discriminator.
References
[1] Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio, “Generative Adversarial Networks,” in Proc. NeurIPS, 2014.
[2] Mehdi Mirza and Simon Osindero, “Conditional Generative Adversarial Nets,” arXiv preprint, arXiv:1411.1784, 2014.
[3] Ishaan Gulrajani, Faruk Ahmed, Martin Arjovsky, Vincent Dumoulin, and Aaron Courville, “Improved Training of Wasserstein GANs,” in Proc. NeurIPS, 2017.
[4] Naveen Kodali, Jacob Abernethy, James Hays, and Zsolt Kira, “On Convergence and Stability of GANs,” arXiv preprint, arXiv:1705.07215, 2017.
[5] Lars Mescheder, Andreas Geiger, and Sebastian Nowozin, “Which training methods for GANs do actually converge?” in Proc. ICML, 2018.
[6] Takeru Miyato, Toshiki Kataoka, Masanori Koyama, and Yuichi Yoshida, “Spectral Normalization for Generative Adversarial Networks,” in Proc. ICLR, 2018.